Exactly where does the Chi-Chi earthquake nucleate?
- Hypocenter Relocation Using the Master Station Method

Honn Kao

Institute of Earth Sciences, Academia Sinica, Nankang, Taipei, Taiwan, ROC

Rong-Yuh Chen and Chien-Hsin Chang

Seismology Center, Central Weather Bureau, Taipei, Taiwan, ROC

also in Institute of Geophysics, National Central University, Chung-Li, Taiwan, ROC

(submitted to TAO Chi-Chi Earthquake Special Issue, March 1, 2000, revised June 10, 2000)

Abstract.   The Chi-Chi earthquake that occurred in central west Taiwan is one of the most well-recorded large earthquakes in the world.  Consequently, one should be able to reliably locate the point of nucleation from the impulsive onsets on short-period seismograms.  But in fact, the hypocentral locations reported by various agencies are different.  Our approach is to relocate the Chi-Chi mainshock with the most unambiguous arrival readings and a 3-D velocity structure using the Master Station (MS) method.  In addition to the usage of a reasonalbe 3-D velocity model, the MS method is superior in two aspects: it is unaffected by the nonlinear nature of traditional earthquake locating process and does not have the trade-off problem between the focal depth and the assumed origin time.  Our results indicate that the best solution of hypocenter always converges to 23.86±0.01°N, 120.81±0.01°E, and depth of 10 km, no matter which initial conditions are adapted.  This location is essentially the same as that later refined by CWB using a combined dataset of both arrivals on short-period seismograms and S-P time intervals measured from near-source strong-motion records.  An important implication of our study is that reliable hypocenter can be derived using as few as 10 accurately determined arrival times from nearby short-period stations when a reasonable 3-D velocity model and the MS method are used in the hypocenter determination.  Thus, the performance of CWB RTD system, which is already the leading example of its kind, can be further improved in the near future.
 

1. Introduction
 

  Hypocentral location is a fundamental parameter in earthquake study.A mislocated hypocenter can cause great uncertainties in many aspects, including the calculations of travel times, epicentral distances, epicentral azimuths and back azimuths…etc.Consequently, studies which depend on these parameters may be significantly affected and can sometimes result in erroneous interpretations (e.g., Kao and Chen, 1991).
 

Because an earthquake fault is of finite dimension, it is sometimes very difficult to associate a particular location as the hypocenter.This is especially true for large earthquakes whose fault dimension can be much larger than the wavelength of the recorded P or S phases (e.g., Billings et al., 1994).For examples, the hypocenter determined from short-period seismograms usually corresponds to the initial phase (or nucleation) of an earthquake rupture, whereas the one from long-period waveforms is associated with the average (or centroid) location of the seismic moment release.For small and moderate-sized events, the rupture dimension is very limited, often on the order of a few km or less (e.g., Kanamori, 1978; Sacks and Rydelek, 1995), such that there is no distinguishable difference between locations of initial rupture and centroid. For large earthquakes, on the other hand, the location of initial rupture can significantly deviate from the centroid hypocenter. Depending on the distribution of seismic moment release, the difference sometimes can be as much as several tens of km.
 

The Chi-Chi earthquake is a very big event along with more than 80 km of surface rupture (Figure 1). Thus, it is expected to have a noticeable difference between the locations of rupture nucleation and centroid. On the other hand, one should be able to reliably locate the point of nucleation from short-period seismograms because of the sharp onsets associated with the earthquake's large magnitude. But in fact, there are some differences among the hypocentral locations reported by various agencies, including the Seismology Center of the Central Weather Bureau (CWB), the U.S. Geological Survey (USGS), and the Harvard University. Which one is the closest to the true nucleation point of the Chi-Chi mainshock? Given the fact that the Chi-Chi earthquake is the most well-recorded (and probably will also be the most well-studied) large event in the Taiwan region, the above question deserves a detailed investigation.
 

It is well known that mislocation of earthquakes can happen if the complex velocity structure is represented by a simple one in the determination of earthquake hypocenters (e.g., Billings et al., 1994; Chiu et al., 1997). So far, all the reported hypocenters for the Chi-Chi earthquake are determined assuming horizontal-layered velocity models. In this study, we try to relocate the Chi-Chi mainshock using unambiguous arrival phases and a three-dimensional (3-D) velocity model (Rau and Wu, 1995). The Master Station (MS) method (Zhou, 1994), which depends on the differential travel times among different stations but not the assumed earthquake origin time, is used in the relocation process. Tests with various subsets of arrival time data are also performed to evaluate the robustness of our results.
 
 
 

2. Reported Hypocenters by Various Agencies
 

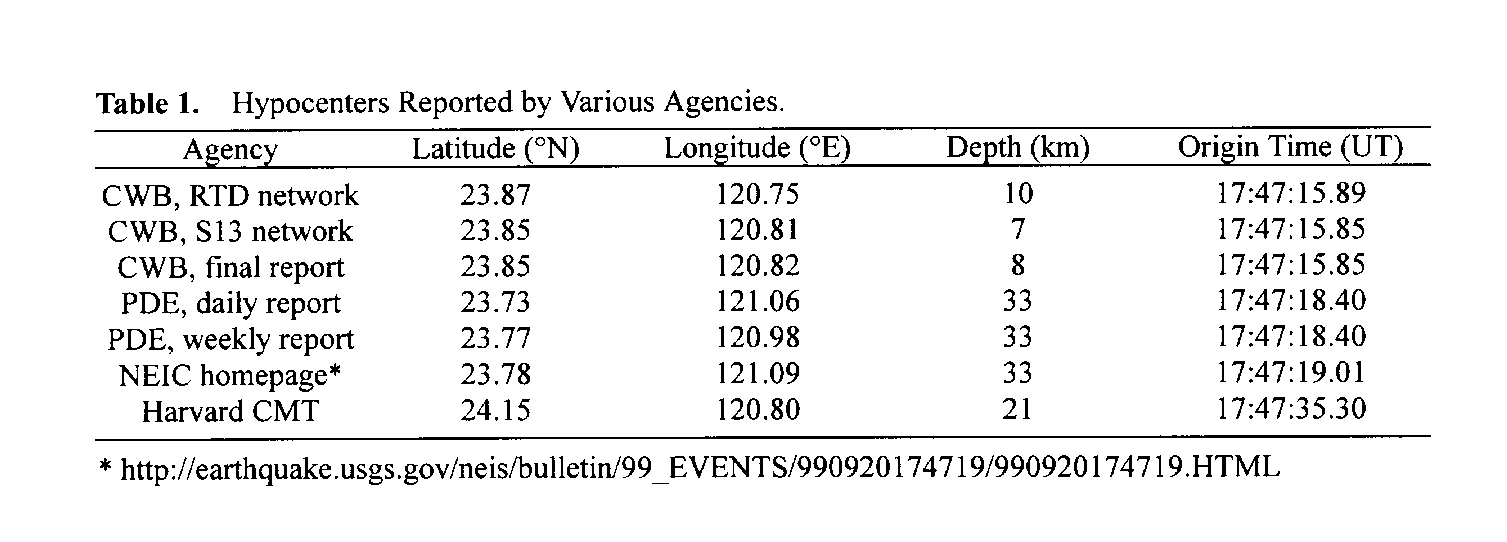
Table 1 and Figure 1 summarize the locations of hypocenters reported by various agencies for the Chi-Chi mainshock.The first report was from the Taiwan Rapid Earthquake Information Release System of CWB (RTD; Wu et al., 1998), which located the epicenter at 23° 52.2'N, 120° 45.00'E, with a depth of 10 km. Because the resolution of epicentral determination depends heavily on the inter-station spacing which is in the order of ~5 km (Shin et al., 2000), it becomes less meaningful to list the epicenter with units <1 km (~0.009°). Therefore, we will limit the spatial resolution in our discussion to one hundredth of a degree hereafter.
 

Using data from the short-period (S13) seismographic network, CWB later revised the epicenter to 23.85°N, 120.81°E – about 5 km to the east of the original report. The focal depth was slightly changed from 10 km to 7 km (Shin et al., 2000). CWB issued the final report at 23.85°N, 120.82°E, with a depth of 8 km, using combined data from both the strong-motion and short-period weak-motion networks.
 

The epicenter listed in the daily report of the Preliminary Determination of Epicenters (PDE) of USGS, which is based on data from global networks, is at 23.73°N, 121.06°E. PDE later shifted the epicenter to 23.77°N, 120.98°E in its weekly report (both the daily and weekly reports are available from the ftp server of the Data Management Center of IRIS). In the homepage of the National Earthquake Information Center (NEIC) of USGS that contains information of all large earthquakes occurred in 1999, the epicenter is listed as 23.78°N, 121.09°E (Table 1).The focal depth of 33 km in all PDE's reports should not be considered as the true depth, but an indication of shallow earthquakes due to the insufficient resolution of the inversion algorithm (Sipkin, 1982).
 

On the other hand, the epicenter reported by the Harvard University, 24.15°N, 120.80°E, is some 30–40 km north of those reported by CWB and USGS. Such a discrepancy is well expected because the location of epicenter is parameterized in the Harvard CMT inversion algorithm (Dziewonski et al., 1981) and presumably corresponds to the centroid of seismic moment release, not the rupture nucleation point. This is also consistent with many preliminary studies showing similar distance interval between the locations of initial rupture and the largest seismic slip (e.g., Chen and Zeng, 1999; Kao and Chen, 2000; Ma et al., 1999).
 
 
 

3. Three-dimensional Relocation: Master Station (MS) Method
 

Our approach is to relocate the Chi-Chi earthquake with the most unambiguous arrival readings and a 3-D velocity structure. Here, we briefly describe the MS method used for such a task. In a nutshell, the advantage of MS method is its capability of locating an earthquake within a given velocity model (certainly including a very complex 3-D one) without frequent recalculation of ray paths and travel times, which turns out to be the most time-consuming process (Zhou, 1994).
 

The conventional way of locating an earthquake is to minimize the sum of square of the residual between the calculated and observed travel times across the seismic network, i.e.,

E(r) = S ( w_j dt_j )², j=1…N(1)
dt_j = T_j - (t(r) + T_o)(2)

where w_j is the weighting factor for station j depending on the quality of data, T_j is the observed arrival time at station j, t_j(r) is the calculated travel time for station j assuming the hypocenter is at r, and T_o is the assumed origin time.
 

There are two major weaknesses associated with the method described above.First of all, because E(r) is a measure of the variance of the residuals which depends on both the location of the hypocenter and the origin time, there is a significant trade-off between the two parameters (e.g., Christensen and Ruff, 1985; Zhou, 1994).The second is that the process is highly nonlinear with respect to the variation of hypocentral coordinates.Thus, there is always a possibility that the inversion is trapped by a local minimum.
 

The trade-off problem is eliminated in the MS method because it determines the hypocenter using the concept of equal differential time (EDT) surfaces.An EDT surface is defined as

S_jk = T_j - T_k = t_j(r) - t_k(r)(3)

if and only if the assumed location of hypocenter, r, is indeed the true location.Therefore, in the process of searching for the best location that satisfies (3), there is no need to assume an origin time.
 

To avoid the nonlinearity problem, the MS method determines the best solution in a forward sense.It is clear that implementing the MS method depends critically on the algorithm that determines the travel times between seismic stations and an assumed hypocenter. Given the computing power of today's workstations, it is not practical to recalculate all the ray paths through a 3-D velocity model in a forward grid search. On the other hand, workstation's input/output (I/O) speed is quite sufficient for searching through a very large database stored on line. Therefore, the first task in the MS method is to systematically calculate the travel times and paths from a set of stations to all the grid points within a given 3-D velocity model and then stores the results on fast I/O hard disks, known as the reference files (Moser, 1991; Zhou, 1994). In other words, the MS method takes advantage of computer's fast I/O performance and big capacity of storage in exchange for computation time later.
 

   In practice, once a set of N observed arrival times is inputted, (N-1) EDT surfaces will be formed and the pre-stored travel-time and ray path reference files will be searched to find out the location(s) passed by the largest number of EDT surfaces. Then the immediate neighborhood of these preliminary locations is searched in grid to find out the best solution that satisfies equation (3). Readers are referred to Moser (1991) and Zhou (1994) for more technical details.
 
 
 

4. Three-dimensional Relocation: Results
 

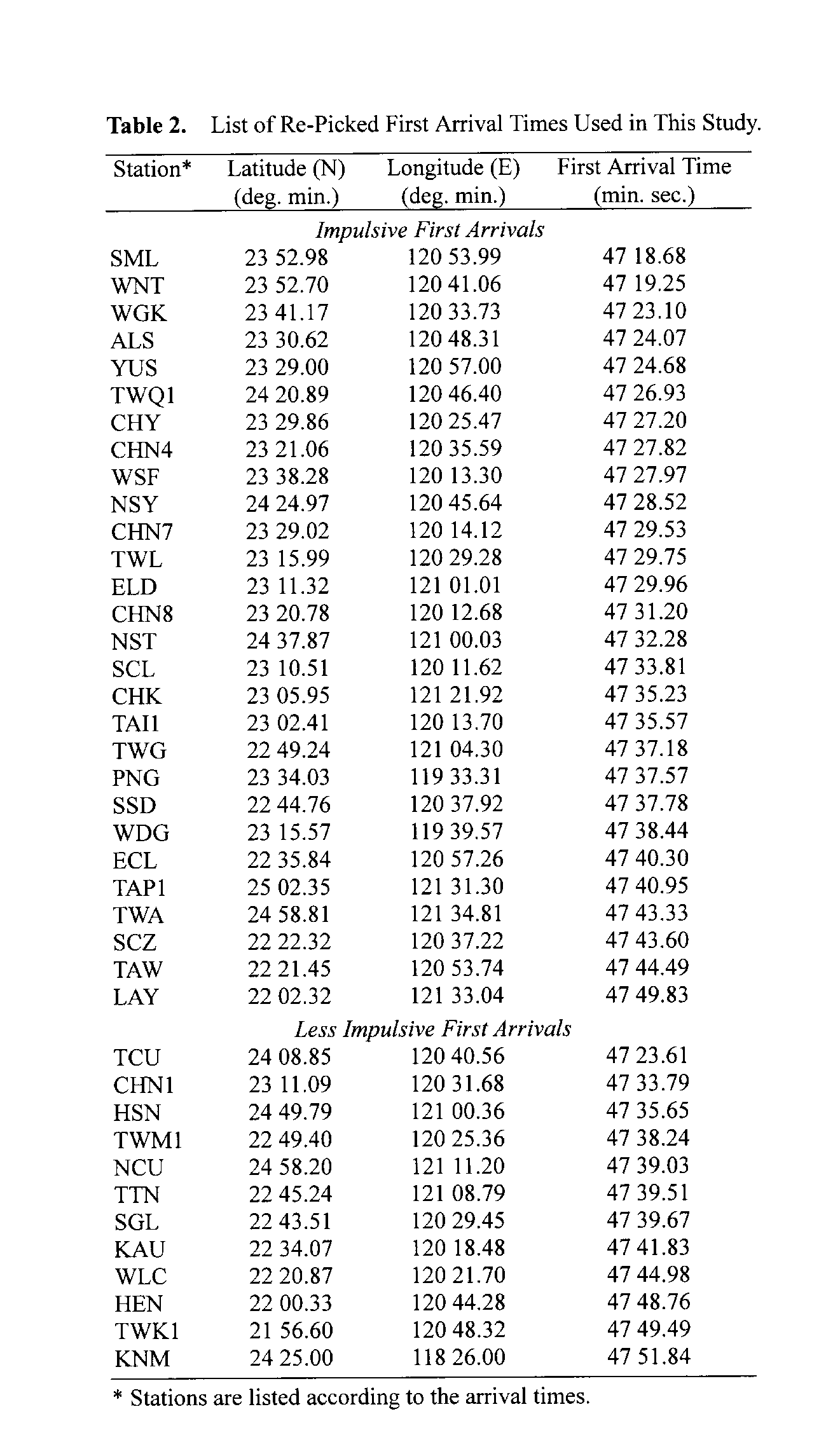
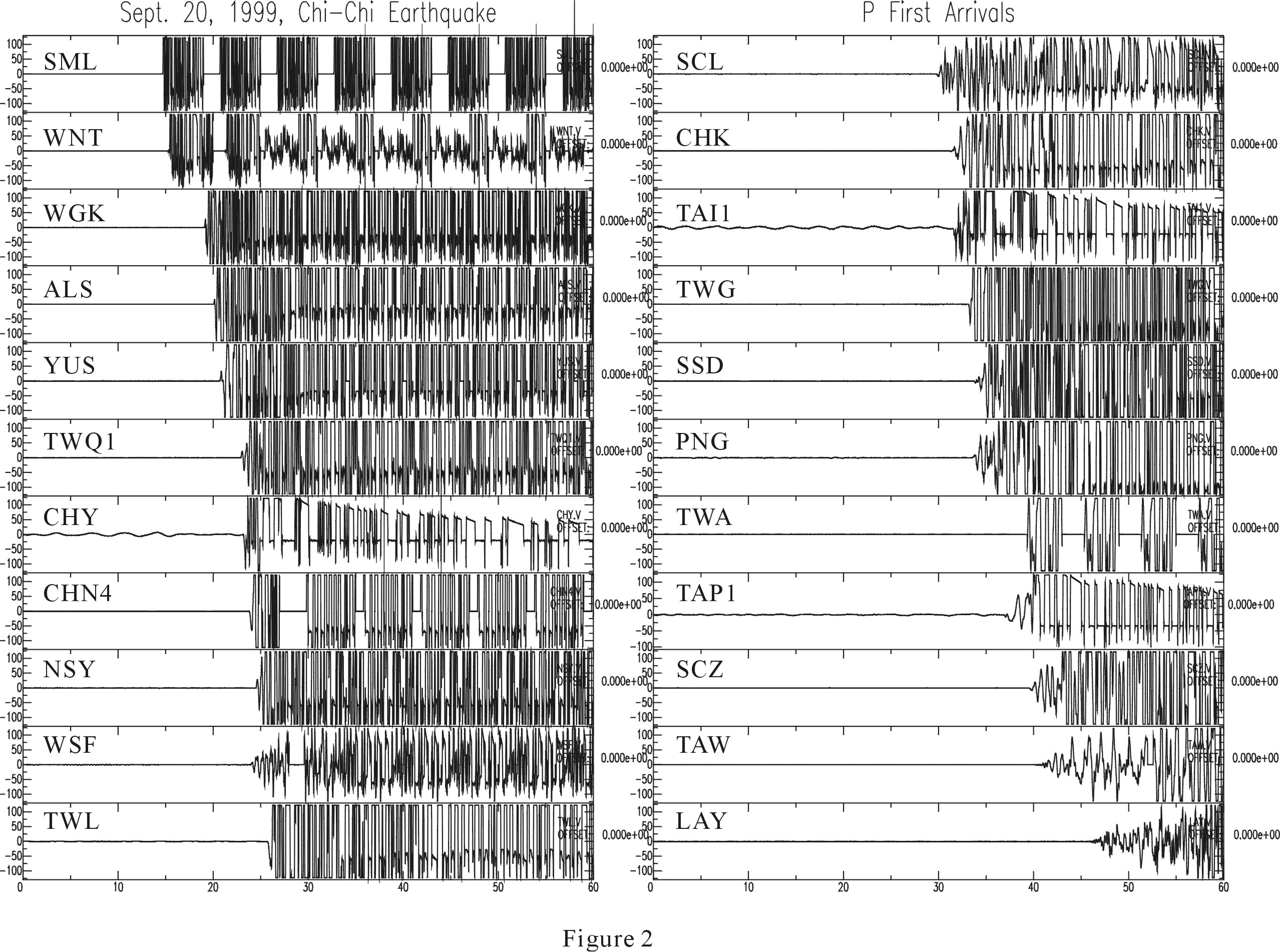
Table 2 is a list of P arrival times that are used in this study. We have personally re-picked all the first arrivals to ensure the highest accuracy. The list is grouped into two categories: one with stations showing impulsive first arrivals such that the identification of the arrival time is unambiguous, and the other with less impulsive first arrivals. Typical examples of seismograms are shown in Figure 2.
 

Due to our insufficient knowledge of the true 3-D velocity model, it is anticipated that stations far away from the epicenter would correspond to larger travel time uncertainties. Previous studies also indicated that, under a couple of specific conditions, a hypocenter determined from a smaller dataset may actually be closer to the true location than that from a larger one (Tsai and Wu, 1997). Such conditions include (1) the velocity structure is very complex and (2) the stations forming the smaller dataset are all within a short distance from the true epicenter. Consequently, we have performed 3-D relocation with various numbers of stations to see if there is any systematic bias in the dataset used in this study. 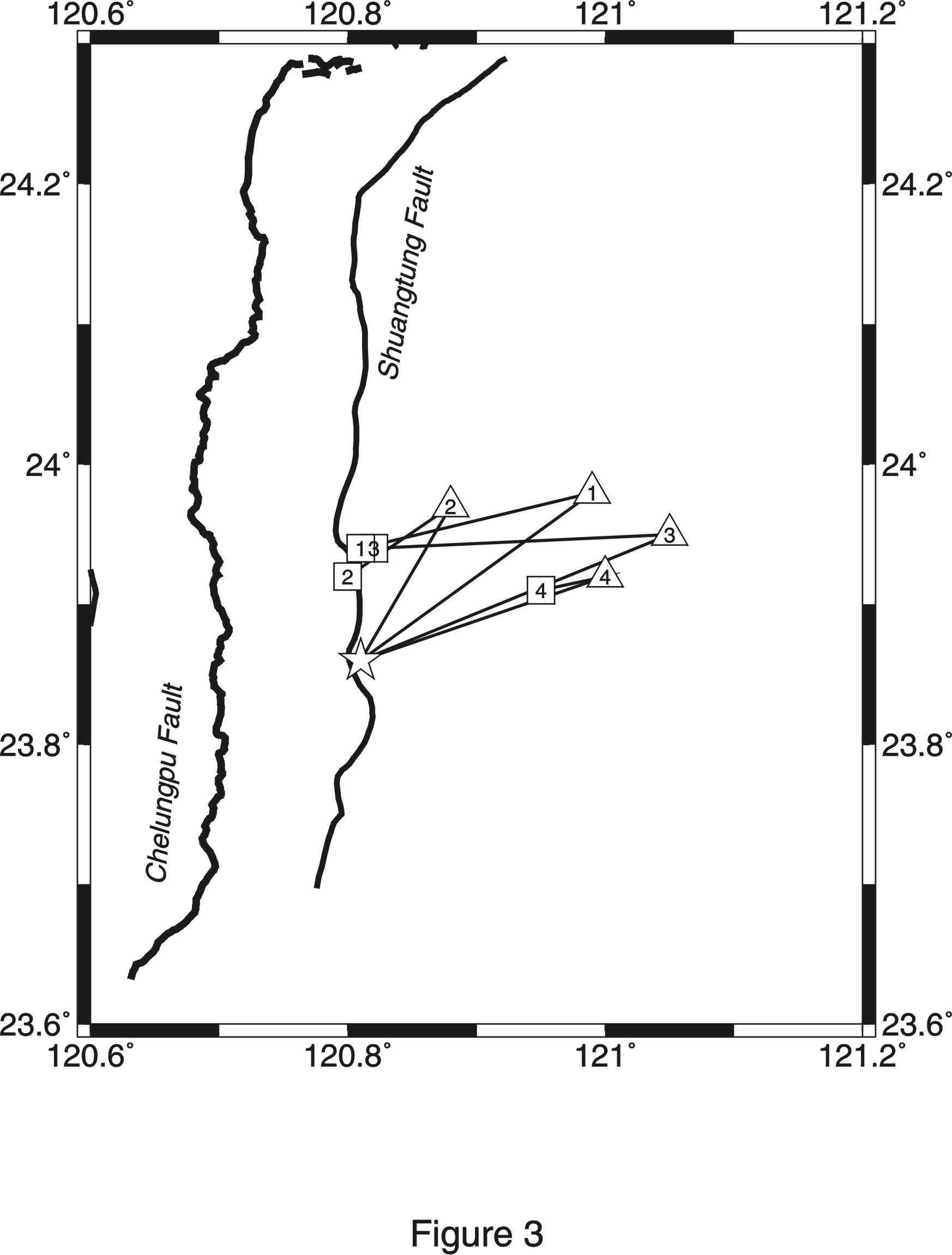Table 3 and Figure 3 show the results of our 3-D relocation. Using arrivals from the first 10 stations (SML-NSY, Table 2), the epicenter is located at 23.86°N, 120.81°E, with a depth of 10 km. This epicenter is ~5 km away from that initially reported by the CWB RTD system, essentially is the same as that in CWB's final report, but is more than 20 km away from that listed in the PDE weekly report (Table 1). The root-mean-square (RMS) travel time residual between the observed and synthetics is very small (0.075 s, Table 3), equivalent to an uncertainty of only 0.5 km. As we increase the number of arrivals used in the process to 20 and 30, the resulted hypocenters migrate slightly to (23.98°N, 120.99°E, depth 30 km) and (23.94°N, 120.81°E, depth 13 km), respectively. Notice that the associated RMS residuals are significantly higher than that in the previous case (2.32 and 2.22 s, respectively). Although an increase in the RMS residual is expected when a larger number of observations is used in the process, such a huge increase (~30 times) may be, at least in part, due to the discrepancies between the 3-D velocity model used (Rau and Wu, 1995) and the realistic velocity structure.
 

Next, instead of using EDT surfaces to determine the preliminary locations, we fix it at that reported by the CWB RTD system (i.e., 23.87°N, 120.75°E, depth 10 km) and perform the finer grid search in the surrounding region. For the maximum ray numbers of 10, 20, and 30, the hypocenters are located at (23.86°N, 120.81°E, depth 10 km), (23.97°N, 120.88°E, depth 28 km), and (23.92°N, 120.80°E, depth 19 km), respectively (Figure 3). If we use the hypocenter determined by the CWB's S13 network (i.e., 23.85°N, 120.81°E, depth 7 km) as the preliminary location, then the results remain similar (Table 3 and Figure 3). Finally, we use the hypocenter listed in the PDE's weekly report as the preliminary location. We obtained again a similar pattern (Table 3 and Figure 3).
 

In general, the focal depth is more difficult to constrain than the location of epicenter because of two reasons. One is the well-known trade-off between the assumed origin time and focal depth, and the other is the limited resolution of travel time curves with respect to depth. Thus, another common way to relocate an earthquake's hypocenter is to set a priori constraint on the focal depth, if reliable and independent estimates are available, and invert only for the epicenter (e.g., Kao and Chen, 1996).
 

Consequently, we modified the MS program such that the focal depth can be fixed during the relocation process. We repeat the above three cases with a given depth at 10, 8, or 12 km, respectively. The results are summarized in Table 3. It is clear that almost all cases with fixed depths bear higher RMS residuals than the ones without. Like in previous cases, results using 10 rays show significantly smaller RMS residuals than that using 20 or more. One important point is that no matter which preliminary location is used in the process, the final location is always at 23.86±0.01°N, 120.81±0.01°E. However, the ones with focal depths fixed at 8 and 12 km have the RMS residuals much higher (2.3 and 2.8 times, respectively) than our best solution (i.e., at 10 km; Table 3), suggesting that the results have sufficient resolution with respect to the focal depth.
 
 
 

5. Discussion and Conclusion
 

From Table 3 and Figure 3, it is quite obvious that no matter how the preliminary locations are selected, the hypocenter with the minimum RMS residual (0.075 s using the earliest 10 arrivals) always converges to 23.86±0.01°N, 120.81±0.01°E, and depth of 10 km. Such results clearly indicate that the process is very stable and virtually free from the nonlinear nature of earthquake relocation. Furthermore, the RMS residual is very sensitive to both the epicenter and focal depth, implying that the combination of this dataset and the MS method has sufficient resolution for such a task.
 

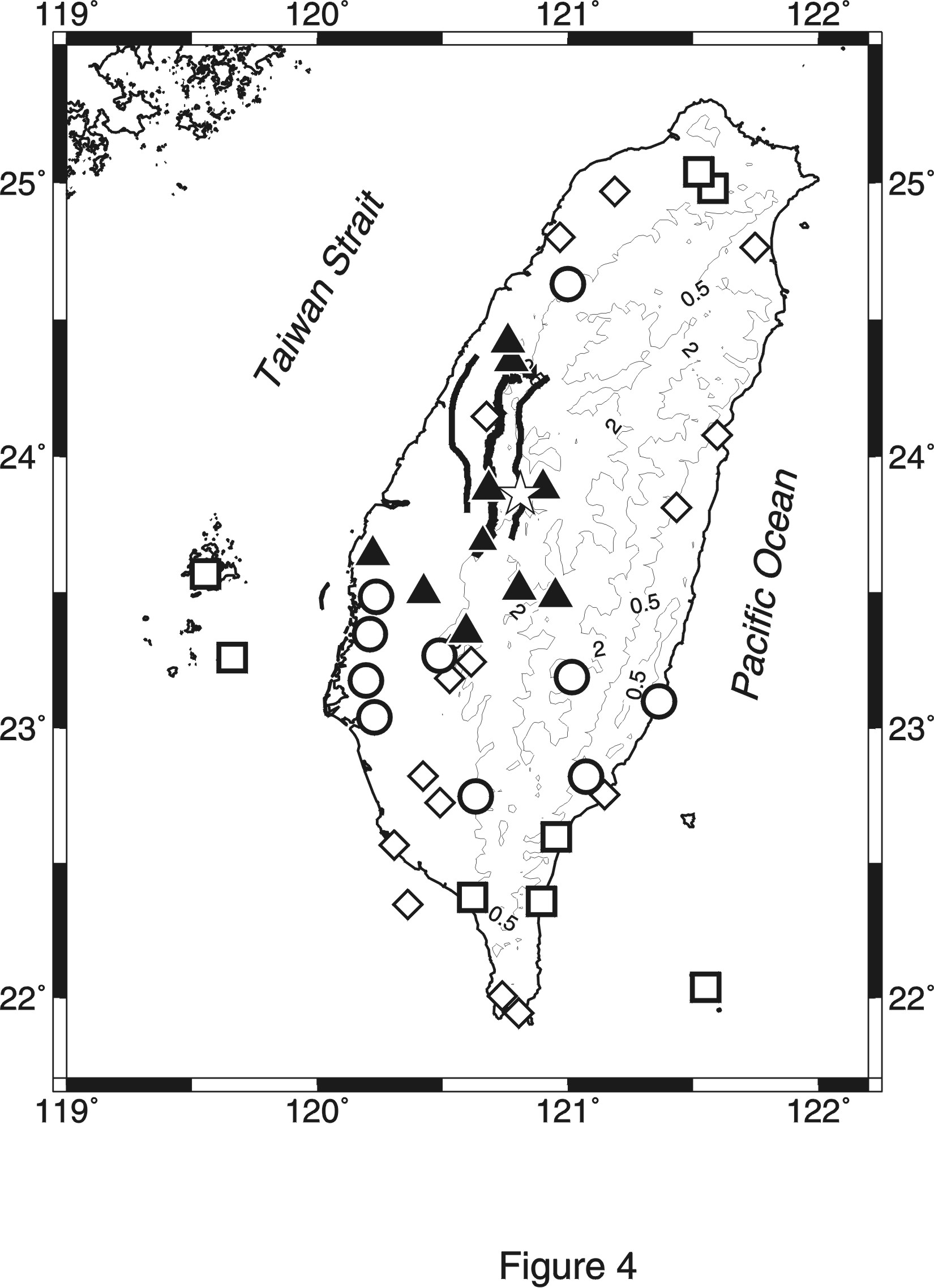
Generally speaking, the RMS travel time residual is proportional to the number of stations used in the relocation. One interesting point in our result, however, is that solutions using 20 arrivals often have larger RMS residuals than that using the whole dataset (Table 3). To investigate the implications of such a phenomenon, we plot out the distribution of seismic stations used in various cases in Figure 4. Clearly, stations of the first 10 arrivals scatter across the central west Taiwan with distances <65 km (Table 2 and Figure 4). The next 10 stations distribute mostly to the south of the epicenter between 70 and 124 km, while the complete dataset covers a wide distance range up to 160 km. It is important to point out that the ray paths connecting the epicenter to stations at the distance range of ~100 km travel mostly within the crust where a significant difference is found between the coastal plain of west Taiwan and the Central Range (Rau and Wu, 1995; Ma et al., 1996). Therefore, we suspect that the less satisfactory results using 20 arrivals are due to the insufficient resolution of the used 3-D velocity model for the large lateral variation within the crust. Furthermore, the better spatial coverage in cases of using 30 stations may also contribute to the better result (e.g., Tsai and Wu, 1997). Obviously, more detailed mapping of regional 3-D velocity structures is warranted in the future. Until a better model becomes available, careful selection of arrival dataset and repeated forward search perhaps are necessary in the 3-D relocation of earthquake hypocenters.
 

Notice that our best solution is almost the same as that in CWB's final report (Tables 2 and 3), although the two results were obtained using completely different approaches. The CWB's final location is determined from a combined dataset of both arrivals on short-period seismograms and S-P time intervals on near-source strong-motion records. An important conclusion of our study is that a reliable hypocenter can be derived using as few as 10 accurately determined arrival times from nearby short-period stations, if a reasonable 3-D velocity model and the MS method are used in the hypocenter determination process. This implies that the performance of CWB RTD system, which is already the leading example of its kind, can be further improved in the near future.
 

Finally, we conduct a test of relocation using all available arrivals, whether impulsive or not, to examine if there is any bias in our preferred dataset (Figure 4). It turns out that the best solution always remains the same. Moreover, the results of various cases (Table 3) show patterns similar to that presented in Figure 2(i.e., cases using 20 arrivals tend to shift to the east, while cases using 30 tend to shift slightly to the north), although the exact locations are a little different from case to case. This result indicates that the relocation is relatively robust even under the influence of some arrivals that are less impulsive.
 
 
 

6. Acknowledgement
 

We benefit form discussions with W.-P. Chen, J.-C. Lee, M. Kikuchi, K.-F. Ma, T. Seno, T. L. Teng, and F. T. Wu. Prof. C.-T. Lee kindly provides the fault traces used in Figures 1, 3, and 4. We also thank Jer-Ming Chiu and an anonymous reviewer for their constructive comments and suggestions. The manuscript is written when one of the authors (HK) is in the Earthquake Research Institute, Univ. of Tokyo, as an invited visiting professor. The facilities and assistance provided by Prof. Yoshio Fukao and his colleagues are greatly appreciated. This research was supported by the National Science Council, ROC, grant NSC 89-2116-M-001 -017 and the Central Weather Bureau, ROC, grand CWB89-2E-06.
 
 

7. References
 
 

Billings, S.D., Sambridge, M.S. and Kennett, B.L.N., 1994. Errors in hypocenter location: Picking, model, and magnitude dependence. Bull. Seismol. Soc.Am., 84: 1978-1990.
 

Chen, C.-H. and Zeng, Y., 1999. Inversion of the source rupture process of the September 20, 1999 Chi-Chi, Taiwan, earthquake (abstract), AGU 1999 Fall Meeting Program: 12.
 

Chiu, J.-M., Chiu, S.-C.C. and Kim, S.G., 1997. The significance of the crustal velocity model in local earthquake locations from a case example of a PANDA experiment in the Central United States. Bull. Seismol. Soc. Am., 87: 1537-1552.
 

Christensen, D.H. and Ruff, L.J., 1985. Analysis of the trade-off between hypocentral depth and source time function. Bull. Seismol. Soc. Am., 75: 1637-1656.
 

Dziewonski, A.M., Chou, T.-A. and Woodhouse, J.H., 1981. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res., 86: 2825-2852.
 

Kanamori, H., 1978. Quantification of earthquakes. Nature, 271: 411-414.
 

Kao, H. and Chen, W.-P., 1991. Earthquakes along the Ryukyu-Kyushu arc:Strain segmentation, lateral compression, and the thermomechanical state of the plate interface. J. Geophys. Res., 96: 21,443-21,485.
 

Kao, H. and Chen, W.-P., 1996. Seismicity in the outer-rise-forearc region and configuration of the subducting lithosphere with special reference to the Japan trench. J. Geophys. Res., 101: 27,811-27,831.
 

Kao, H. and Chen, W.-P., 2000. The Chi-Chi earthquake sequence of September 20, 1999 in Taiwan: Seismotectonics of an active, out-of-sequence thrust. Science, submitted.
 

Ma, K.-F., Wang, J.-H. and Zhao, D., 1996. Three-dimensional seismic velocity structure of the crust and uppermost mantle beneath Taiwan. J. Phys. Earth, 44: 85-105.
 

Ma, K.-F., Song, D.-R. and Mori, J., 1999. Teleseismic and near source motion investigation of the September 20, 1999 Chi-Chi Taiwan earthquake (abstract). AGU 1999 Fall Meeting Program: 12.
 

Moser, T.J., 1991. Shortest path calculation of seismic rays. Geophysics, 56: 59-67.
 

Rau, R.-J. and Wu, F.T., 1995. Tomographic imaging of lithospheric structures under Taiwan. Earth Planet. Sci. Lett., 133: 517-532.
 

Sacks, I.S. and Rydelek, P.A., 1995. Earthquake "quanta" as an explanation for observed magnitudes and stress drops. Bull. Seismol. Soc. Am., 85: 808-813.
 

Shin, T.C., Kuo, K.W., Lee, W.H.K., Teng, T.L. and Tsai, Y.B., 2000. A preliminary report on the 1999 Chi-Chi (Taiwan) earthquake. Seismol. Res. Lett., 71: 23-29.
 

Sipkin, S.A., 1982. Estimation of earthquake source parameters by the inversion of waveform data: synthetic waveforms. Phys. Earth Planet. Inter., 30: 242-259.
 

Tsai, Y.-B. and Wu, H.-H., 1997. A study of the errors in locating earthquakes due to the geometry of the Taiwan seismic network. Terr. Atmos. Oceanic Sci., 8: 355-370.
 

Wu, Y.-M., Shin, T.-C. and Tsai, Y.-B., 1998. Quick and reliable determination of magnitude for seismic early warning. Bull. Seismol. Soc. Am., 88: 1254-1259.
 

Zhou, H.-W., 1994. Rapid three-dimensionaal hypocentral determination using a master station method. J. Geophys. Res., 99: 15,439-15,455.